一种节省空间的基于递归的线段树实现
使用先序遍历的节点访问顺序重新给左右儿子编号,大大节省了空间
自古以来,实现线段树所需要的数组空间大小有着比较激烈的争论。一种基于递归的线段树实现认为至少需要$\mathcal{O}(4n)$的空间,而另一种基于直接循环的方法认为其实只需要$2n-1$的空间。关于为什么基于递归的方法需要$\mathcal{O}(4n)$的严格证明可以去网上搜索,或者这里提供了一个简易的证明方法。总的来说,基于递归的线段树实现起来更加直观,但由于dummy node的存在造成了空间的浪费。而基于直接循环的方法对实现的要求更高。本文介绍了一个基于递归的线段树实现,通过改变每个节点的左右儿子的编号高效的利用了空间,使得基于递归的线段树也只需要$2n-1$的空间。另外,关于基于循环的线段树实现方法,可以参考这篇博客。
要回答为什么dummy node的存在导致了基于递归的线段树需要$\mathcal{O}(4n)$的空间,我们得先了解一下传统的实现方式。
传统实现
我们考虑一个恰好为$2^k$的序列,由于长度恰好为2次幂,因此线段树的每个节点的长度恰好是它父亲节点的一半,因此最后形成的线段树是一颗满二叉树。比如下图是一颗长度为8的序列组成的线段树,维护了区间$min$的查询。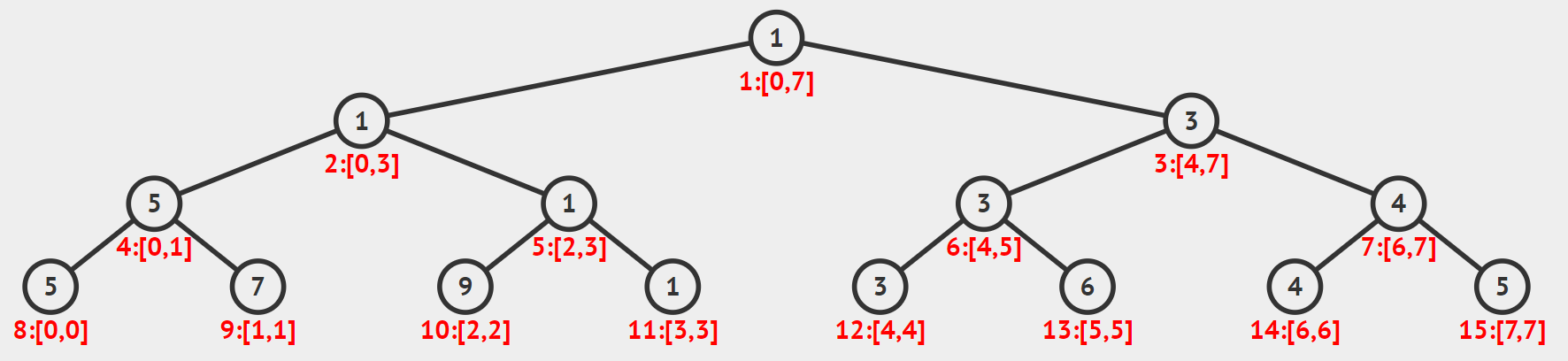
我们还可以注意到,如果根节点的编号是1的话,那么对于每个非叶子节点$x$,它的左儿子是$2x$,右儿子是$2x+1$。整个线段树的节点个数是$2n-1$。我们的build()函数可以大致这么实现。
1 | template<typename Container> |
那么很自然地我们就会想到,如果对于一个长度不是$2^k$的序列,上述结论是否依然成立呢?答案是显然的,很自然地,我们依然可以将每个非叶子节点的左儿子设置成$2x$,右节点设置成$2x+1$。那么对于一颗长度为10的序列组成的线段树,就会变成下图所示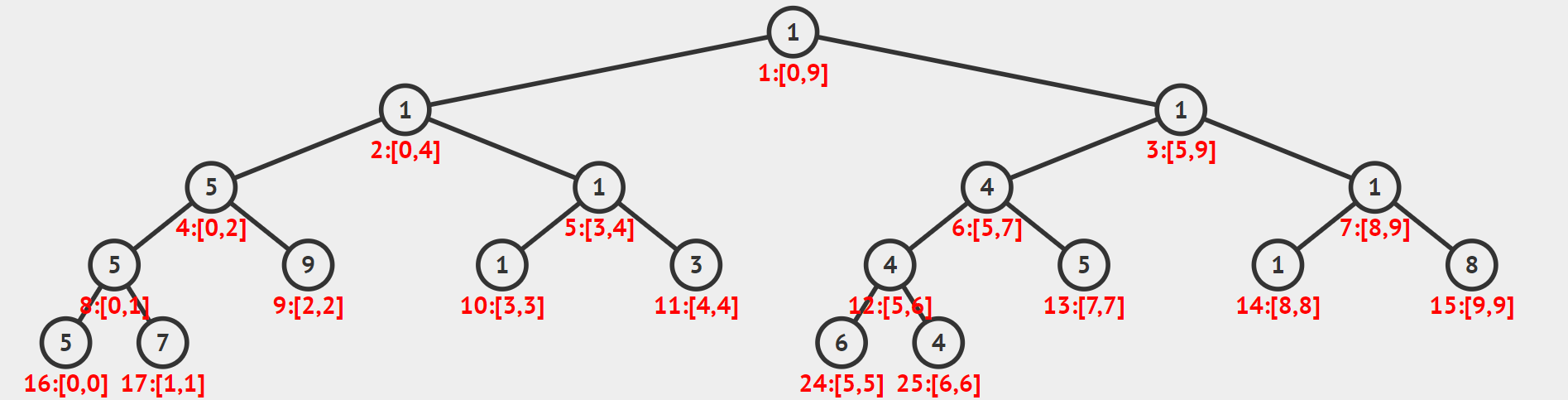
我们大致可以得出两个结论。第一,如果你去统计这颗线段树的节点个数,你会发现它依然是$2n-1$。这个是很容易理解的,因为任何一个$[1,n]$的序列,它一定有$n-1$个分割点,那么要全部变成长度为1的叶子节点,它必然要经历$n-1$次分割,加上叶子节点的个数$n$,总节点自然就是$2n-1$了。因此我们可以得出一个重要结论
长度为$n$的序列会形成$2n-1$个节点个数的线段树。
这个结论非常重要,之后我们还会用到,因此需要暂时把它记住。至于第二个结论,就是从图中我们发现有些节点是不存在的,比如18-23号节点,另外24和25号节点的编号实际上已经超过了$2n-1$,这就是为什么本文开头提到基于递归的线段树需要$\mathcal{O}(4n)$的空间的原因。
那么既然线段树的总节点树就是$2n-1$,我们是否可以通过某种办法,把这些节点的编号重新映射一下,使得线段树中每个节点的编号都落在$2n-1$内,这样我们就不需要开$\mathcal{O}(4n)$的空间了,并且每个空间也能充分得到利用了,岂不美哉?
按照先序遍历重新编号节点
答案是肯定的,比如我们可以按照整棵树的节点访问顺序,也就是先序遍历的顺序给节点重新编号。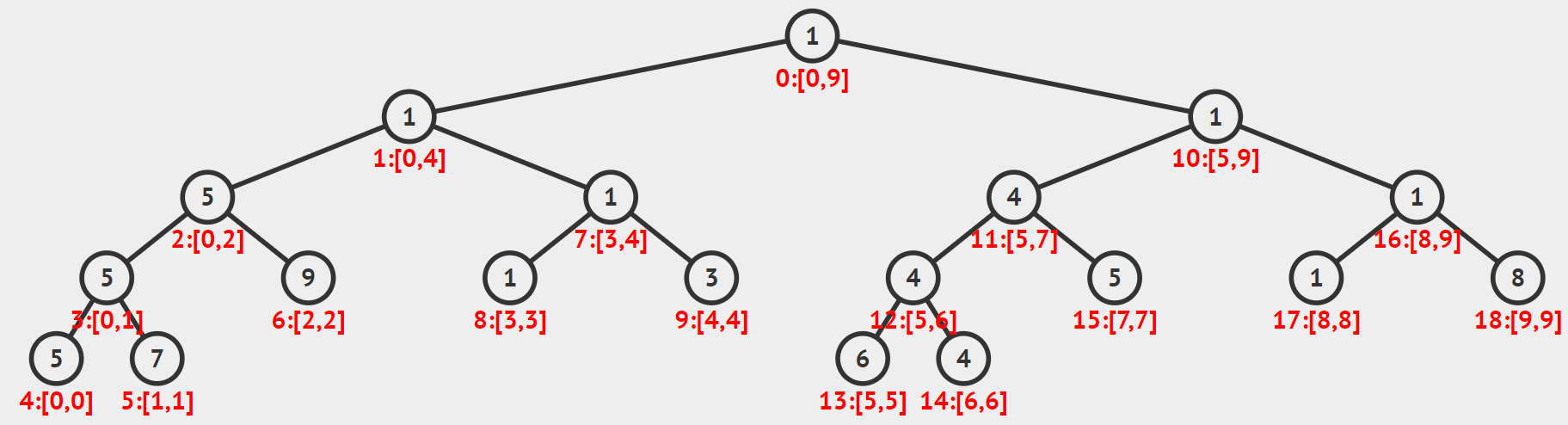
我们不再使用$2x$和$2x+1$给左右儿子编号了,而是使用从根节点开始,实际访问每个节点的顺序,也就是先序遍历的顺序给每个节点编号,或者再换一个说法,就是dfs的访问顺序。这样每个节点在数组空间中的排列就是紧密的了,那我们就只需要开$2n-1$的数组大小就能完成整颗线段树的构建了。
那么说了那么多,问题来了。我在递归遍历的时候怎么求出左右儿子的编号呢?本来只要$2x$和$2x+1$就能很容易的求出了,现在这么一搞,我怎么知道左右儿子的编号是多少呢?难不成我还要搞一个全局计数器去记录节点编号吗?
并不需要。首先我们来看左儿子的编号,因为现在的编号顺序就是实际的访问顺序了,而左儿子恰恰就是要访问的下一个节点,那么显然,左儿子的编号就是$x+1$了。那么右儿子呢?其实也很简单,我们注意到,如果左儿子划分了$[l,r]$这个区间,那么实际上左儿子就是一颗划分了$[l,r]$序列的子线段树。还记得之前的结论吗?$[l,r]$的区间长度是$r-l+1$,划分了$r-l+1$的长度会形成$2(r-l+1)-1$个节点个数。因此如果当前节点是$x$,它的左子树就有$2(r-l+1)-1$个节点,而右儿子恰好就是左子树全部遍历完之后的下一个节点,因此右儿子的节点编号就是$x+2(r-l+1)-1+1$,也就是$x+2(r-l+1)$了。而$l,r$这些值在我们遍历的时候都是自然维护了,所以计算左右儿子都不需要引入任何额外的变量。build()代码如下所示
1 | template<typename Container> |
注意到相比之前的代码,我们仅仅是修改了左右儿子的节点编号lc和rc而已。
结论
虽然开$4n$的空间实际上并不会有什么太大的影响,但使用新的节点编号方法并不会增加任何代码的复杂度,相反还能节省一半的空间,因此在我看来这种方式更加优雅。从另一个角度来说,将线段树的数组空间排列紧密化可以更好地利用局部性原理,在某种意义上对性能有一定的提升。
参考
上述思想参考了tourist大神的线段树代码,在此默默表示感谢。
一种节省空间的基于递归的线段树实现

